Imago & Nucleus 像与核
〔定义〕:
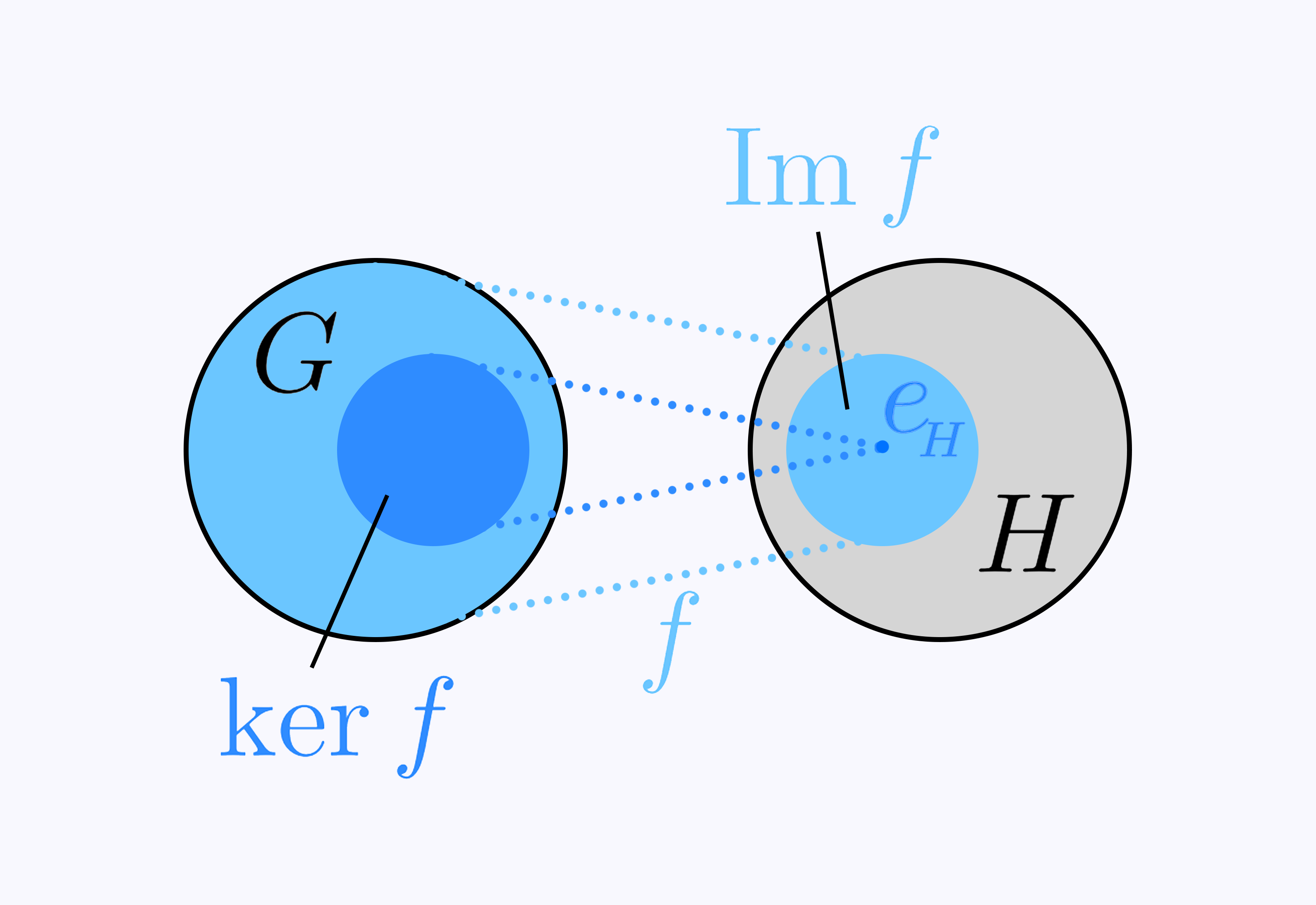
设 $f:G\to H$ 是群之间的映射:
$f(G):=\{f(g)\mid g\in G\}$ 称为群 $G$ 在映射 $f$ 下的像(image),即 $G$ 中所有元素经过映射 $f$ 所得结果所成集合,它是 $H$ 的子集.特别地,若 $f$ 为群同态,则称之为同态 $f$ 的像,记为 $\operatorname{Im} f$.
设 $A\subseteq H$,则 $\{g\in G\mid f(g)\in A\}$ 称为子集 $A$ 在映射 $f$ 下的原像、前像(preimage)或逆像(inverse image).
若 $f$ 为群同态,$\{g\in G\mid f(g)=e_H\}$ 称为同态 $f$ 的核(kernel),记为 $\ker f$.对于一个 $G$ 到 $H$ 的同态,其核即 $H$ 中单位元所成单元素集合 $\{e_H\}$ 在映射 $f$ 下的原像.
Theoremata Homomorphismi
同构定理
〔定理 7.1〕 同态基本定理(fundamental theorem on isomorphism)或第一同构定理(first isomorphism theorem)(1):(本段下文均记 $e$ 为 $G$ 的单位元,$e’$ 为 $H$ 的单位元.)
设 $G,\,H$ 为群,$\varphi:G\to H$ 为群同态,则有
(α) $\ker \varphi\unlhd G$;
(β) $\operatorname{Im}\varphi\leq H$;
(γ) $\operatorname{Im}\varphi\cong G/\ker \varphi$.
〔证明〕 :
(α):
$\forall\;a,\,b\in\ker \varphi,\quad \varphi(a)=\varphi(b)=e’$,
因为 $\varphi(a^{-1})=\varphi(a)^{-1}=e’$ (群同态的性质),
所以 $a^{-1}\in\ker \varphi$,
又有 $\varphi(a^{-1}b)=\varphi(a^{-1})\varphi(b)=e’e’=e’$,
从而 $a^{-1}b\in\ker \varphi$,
得知 $\ker \varphi\leq G$.
又 $\forall\;g\in G,\, a\in\ker \varphi,$
$\varphi(g^{-1}ag)=\varphi(g^{-1})\cdot e’\cdot\varphi(g)=e’$ $=\varphi(g)\cdot e’\cdot\varphi(g^{-1})=\varphi(gag^{-1})$,
所以 $g^{-1}ag,\,gag^{-1}\in\ker \varphi$,
从而 $g^{-1}(\ker \varphi)g\subseteq\ker \varphi$,且 $g(\ker \varphi)g^{-1}\subseteq \ker \varphi$,
于是又有 $\ker \varphi\subseteq g^{-1}(\ker \varphi)g$,
由此得 $\forall\;g\in G,\quad\ker \varphi=g^{-1}(\ker \varphi)g$,即得证 $\ker \varphi\unlhd G$.
(β):
$\forall\;a,\,b\in\operatorname{Im}\varphi,$
$\exists\;\alpha,\,\beta\in G,\quad\varphi(\alpha)=a,\;\varphi(\beta)=b$,
则 $\exists\;\alpha^{-1}\in G,\quad\varphi(\alpha^{-1})=\varphi(\alpha)^{-1}=a^{-1}\in\operatorname{Im}\varphi$,
又 $\exists\;\alpha^{-1}\beta\in G,\quad\varphi(\alpha^{-1}\beta)=a^{-1}b\in\operatorname{Im}\varphi$,
得证 $\operatorname{Im}\varphi\leq H$.
(γ):
定义映射 $\overline\varphi:G/\ker \varphi\to\operatorname{Im}\varphi,\quad\overline g\mapsto\varphi(g)$,其中 $\overline g:=g(\ker \varphi)=(\ker \varphi)g\in G/\ker \varphi$.
设 $g’\in g(\ker \varphi)$,则 $\exists\;k\in\ker \varphi,\quad g’=gk$,
于是 $\overline\varphi(\overline{g’})=\varphi(g’)=\varphi(gk)=\varphi(g)\varphi(k)=\varphi(g)=\overline\varphi(\overline g)$,
由此可知该映射定义良好.
又可证 $\overline\varphi$ 为群同态:
$\overline\varphi(\overline g\cdot\overline{g’})=\overline\varphi(\overline{gg’})=\varphi(gg’)=\varphi(g)\varphi(g’)=\overline\varphi(g)\overline\varphi(g’)$.
又有 $\forall\;a’\in\operatorname{Im}\varphi,\;\exists\;a\in G,\quad \varphi(a)=a’$,
于是 $\overline\varphi(\overline a)=\varphi(a)=a’$,
得证 $\overline\varphi$ 为满同态.
又设 $a,\,b\in G$,若 $\overline a,\,\overline b\in G/\ker \varphi$,且 $\overline\varphi(\overline a)=\overline\varphi(\overline b)$,则 $\varphi(a)=\varphi(b)$,
从而 $\varphi(a^{-1}b)=\varphi(a^{-1})\varphi(b)=e’$,
进而 $a^{-1}b\in\ker \varphi$,且 $a(\ker \varphi)=b(\ker \varphi)$,
即 $\overline a=\overline b$,得证 $\overline\varphi$ 为单同态.
综上,$\overline\varphi$ 为群同构,即得证 $\operatorname{Im}\varphi\cong G/\ker \varphi$.
■
- 这里所定义的映射 $\overline\varphi$ 称为典范同构(canonical isomorphism).另外,若设映射 $\psi:G/\ker \varphi\to H$,则可证 $\psi$ 为单同态,称为典范单同态(canonical monomorphism).
〔同态基本定理的推论〕 :
设 $\varphi:G\to H$ 是群同态,则
(α) $\varphi$ 为单同态 $\Leftrightarrow$ $\ker \varphi=\{e\}$;
(β) $\varphi$ 为满同态 $\Leftrightarrow$ 存在典范同构 $\overline\varphi:G/\ker \varphi\overset{\Large\sim}\to H$.
〔证明〕 :
(α):
〔$\Rightarrow$〕显然.
〔$\Leftarrow$〕:
由于 $\forall\;a,\,b\in G,\quad\varphi(a)=\varphi(b)\;\Rightarrow\;\varphi(a^{-1}b)=e’$,
所以 $a^{-1}b\in\ker \varphi=\{e\}$,
于是 $a^{-1}b=e$,即 $a=b$,得证 $\varphi$ 为单同态.
(β):
此时 $\operatorname{Im}\varphi=H$,显然得证(同态基本定理 (γ)).
■
- 同态基本定理在线性空间上的表现形式即为秩–零化度定理(rank–nullity theorem).
〔例〕 :
记 $a\in\mathbb Z$ 的模 $n$ 同余类为 $[a]$,映射 $f:\mathbb Z\to\mathbb Z_n,\quad a\mapsto[a]$ 为加法群满同态,且 $\ker f=n\mathbb Z:=\{nk\mid k\in\mathbb Z\}$(即 $n$ 的全体倍数所成集合).于是有典范同构 $\mathbb Z/n\mathbb Z\cong \mathbb Z_n$,因此在很多场合下会把整数模 $n$ 加法群 $\mathbb Z_n$ 记作 $\mathbb Z/n\mathbb Z$.
设映射 $\delta:\mathrm{GL}_n(\mathbb R)\to\mathbb R\setminus\{0\},\quad 𝑴\mapsto\det(𝑴)$ 为乘法群满同态,且 $\ker \delta=\mathrm{SL}_n(\mathbb R)\lhd\mathrm{GL}_n(\mathbb R)$,且 $\mathrm{GL}_n(\mathbb R)/\mathrm{SL}_n(\mathbb R)\cong\mathbb R\setminus\{0\}$.
〔定理 7.2〕对应定理(correspondence theorem),格定理(lattice theorem)或第四同构定理(fourth isomorphism theorem)(2):
设 $N\unlhd G$,$\overline G:=G/N$,$\mathscr M=\{M\mid N\leq M\leq G\}$ (“介于”$G$ 与 $N$ 的所有子群之集族),$\overline{\mathscr M}=\{H\mid H\leq \overline G\}$.则映射 $f:\mathscr M\to\overline{\mathscr M},\quad M\mapsto\overline M:=M/N$ 为双射,且对于任意 $M\in \mathscr M$,有以下命题成立:
(α) $M\unlhd G\;\Leftrightarrow\; \overline M\unlhd \overline G$ (正规保留性);
(β) $\forall\;M’\in\mathscr M,\quad M\leq M’\;\Leftrightarrow\; \overline M\leq \overline {M’}$ (偏序保留性);
(γ) $\forall\;M’\in\mathscr M,\;M\leq M’,\quad[M’:M]=[\overline{M’}:\overline M]$ (指数保留性).
〔证明〕:
不难证明,$\overline M\leq\overline G$ 成立.
若要定义映射 $h:\overline{\mathscr M}\to \mathscr M,\quad \overline{M}\mapsto\{g\in G\mid gN\in \overline M\}$,需要验证 $h(\overline M)\leq G$:
若 $\overline M\in\overline{\mathscr M}$,设任意 $a,\,b\in h(\overline M)$,则有 $aN,\,bN\in \overline M$.
因为 $\overline M\leq \overline G$,所以对于所有 $aN,\,bN\in\overline M$,都有 $(a^{-1}b)N\in\overline M$,
所以 $a^{-1}b\in h(\overline M)$,这就验证了 $h(\overline M)\leq G$.
$\forall\;g\in N,\quad gN=N\in \overline M$,
所以 $g=h(\overline M)$,从而 $N\subseteq h(\overline M)$,
进而可得
$fh(\overline M)=f(\{g\in G\mid gN\in \overline M\})=\overline M$,
$hf(M)=h(\overline M)=M$,
于是可知 $f$ 与 $h$ 是互逆的映射,所以 $f$ 为双射.
在此基础上可以证明
(α):(需要注意 $N\unlhd G,\;N\leq M\leq G\;\Rightarrow\;N\unlhd M$)
$\begin{aligned} M\unlhd G\;&\Leftrightarrow\;\forall\;g\in G,\quad gM=Mg \\
\phantom{\dfrac11}&\Leftrightarrow\;\forall\;gN\in \overline G,\quad gN\overline M=\overline MNg\\
&\Leftrightarrow\;\overline M\unlhd \overline G.\end{aligned}$(β) 显然成立.
(γ):
设 $M’=\displaystyle\bigsqcup_{i=1}^k\;p_iM\;(p\in M’)$,
而 $\overline{M’}=\{\mu N\mid \mu\in M’\}$,$\overline M=\{mN\mid m\in M\}$,
对于任一 $\mu\in M’$,均存在 $m\in M,\;p\in M’$ 使得 $\mu=pm$,
于是 $\overline{M’}=\{p_imN=p_i\overline M\mid m\in M,\,p_i\in M’,\;1\leq i\leq k\}$ $=\displaystyle\bigsqcup_{i=1}^k\;p_imN=\bigsqcup_{i=1}^k\;p_i\overline M$,
所以 $[M’:M]=[\overline{M’}:\overline M]=k$.
■
〔定理 7.3〕 第二同构定理(second isomorphism theorem):
设 $N\unlhd G,\;H\unlhd G$,则
$(H\cap N)\unlhd H$,$N\unlhd NH\leq G$,$NH/N\cong H/(H\cap N)$.
〔证明〕:
$N\unlhd G\;\Rightarrow\; \forall\;h\in H,\quad hN=Nh$,
所以 $\forall\;n,\,n’\in N,\;h,\,h’\in H,$
$(nh)^{-1}(n’h’)=h^{-1}n^{-1}n’h’=(n^{-1}n’)(h^{-1}h’)\in NH$,
所以 $NH\leq G$,
因为 $N\unlhd G$,所以 $N\subset NH\subset G$,进而 $N\unlhd NH$.
考虑映射 $f:H\to NH/N,\quad h\mapsto Nh$(3),
易证该映射为满同态,且 $\ker f=\{h\in H\mid f(h)=N\}=\{h\in H\mid h\in N\}=H\cap N$,
由同态基本定理,则有 $H\cap N=\ker f\unlhd H$,$NH/N\cong H/(H\cap N)$.
■
〔定理 7.4〕 第三同构定理(third isomorphism theorem):
设 $M,\,N\unlhd G,\;N\leq M$,
则 $G/M\cong (G/N)/(M/N)$ (或写作 $\dfrac{G/N}{M/N}$).
(注意 $N\unlhd G,\;N\leq M\;\Rightarrow\;N\unlhd M$,且由对应定理,$M/N\unlhd G/N$.)
〔证明〕:
设映射 $f: G/N\to G/M,\quad gN\mapsto gM$,验证该映射定义良好:
$\forall\;g,\,g’\in G,$
$gN=g’N\;\Rightarrow\;g^{-1}g\in N\subseteq M$ $\Rightarrow\;g^{-1}g\in M\;\Rightarrow\;gM=g’M$.
进而可知 $f$ 为满同态,于是对任意 $g\in G$,
$gN\in\ker f\;\Leftrightarrow\;gM=M$ $\Leftrightarrow\; g\in M\;\Leftrightarrow\; gN\in M/N$,
从而 $\ker f=M/N$,
由同态基本定理有 $(G/N)/\ker f\cong \operatorname{Im} f$,
即 $(G/N)/(M/N)\cong G/M$.
■
Annotationes 注释
(1). 与同构相关的定理,其命名在各种文献中有所差异,尤其是使用序号者.这里采用比较常用的命名. ↩
(2). 对应定理有更普遍的表述,这里考虑了其一种情况. ↩
(3). $NH/N=\{Nnh\mid nh\in NH\}=\{Nh\mid h\in H\}$. ↩